史密斯预估补偿控制

被控对象含纯滞后环节的闭环传递函数：

\begin{array}{r} G (s) = G_{0} (s) e^{- τ s} W (s) = \frac{D (s) G_{0} (s) e^{- τ s}}{1 + D (s) G_{0} (s) e^{- τ s}} \end{array}

注意这里是将被控对象不包含纯滞后的部分作为 $G_{0} (s)$

造成系统难以控制的本质是特征方程中含有纯滞后环节

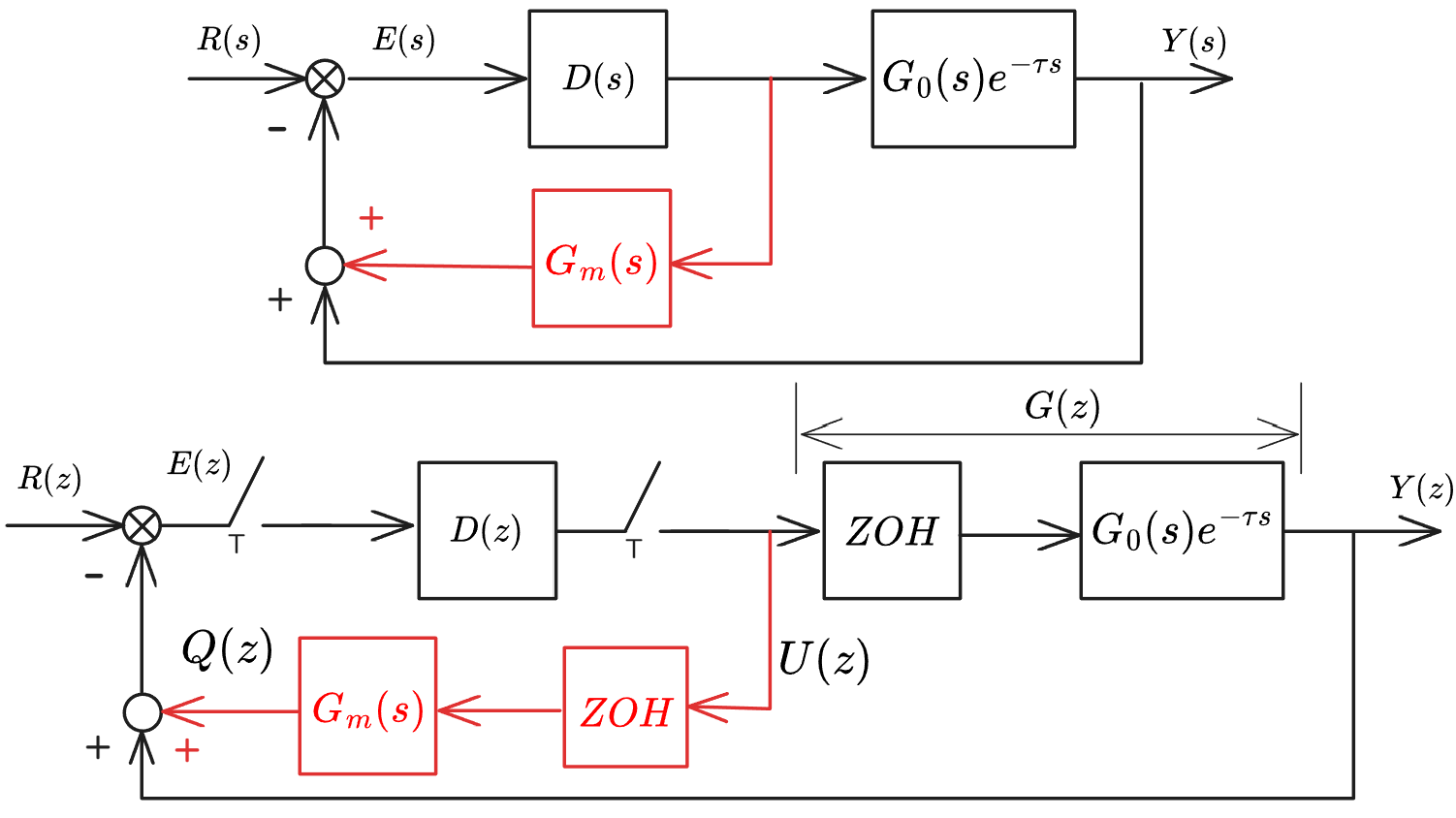
引入与含纯滞后环节的被控对象并联的补偿器，称为史密斯预估补偿器 $G_{m} (s)$ :

\begin{array}{r} W_{1} (s) = \frac{D (s) G_{0} (s) e^{- τ s}}{1 + D (s) G_{0} (s) e^{- τ s} + D (s) G_{m} (s)} = \frac{D (s) G_{0} (s) e^{- τ s}}{1 + D (s) G_{0} (s)} \Rightarrow G_{m} (s) = G_{0} (s) (1 - e^{- τ s}) \end{array}

对补偿器乘以零阶保持器进行离散化

\begin{array}{r} G_{m} (z) = Z [G_{m} (s) G_{h} (s)] = Z [G_{0} (s) (1 - e^{- τ s}) \frac{1 - e^{- T s}}{s}] = (1 - z^{- 1}) (1 - z^{- N}) Z [\frac{G_{0} (s)}{s}] N = \frac{τ}{T} \end{array}

再写为控制算法的形式：

\begin{array}{r} G_{m} (z) = \frac{Q (z)}{U (z)} \Rightarrow q (k) = Z^{- 1} [G_{m} (z) U (z)] \end{array}

Important

千万要注意题目的表达 ! 不要被符号搞混了
要注意给的被控对象可能直接写为 $G_{0} (s)$ , 要把其中的纯滞后提出来！

\begin{array}{r} e^{- τ s} \approx \frac{1 - \frac{1}{2} τ s + \frac{1}{8} τ^{2} s^{2}}{1 + \frac{1}{2} τ s + \frac{1}{8} τ^{2} s^{2}} \end{array}